|
|
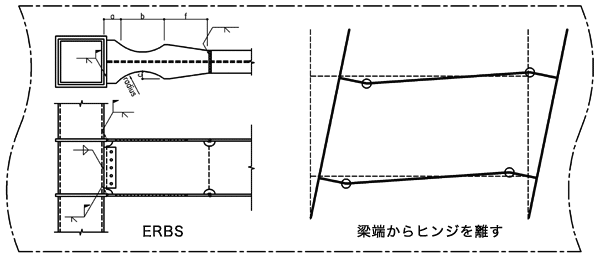
ERBS工法の設計フロー |
| |
① 梁形状の設定
|
| |
RBS工法の形状・寸法は、実験・解析結果ならびにFEMA-350(文献1)を準用して、表1~2および図
1~3のように定める。
|
|
表1 構成要素の形状寸法 |
 |
| (文献1) |
米国鉄骨耐震規準「FEMA-350, Recommended Seismic Design Criteria for New Steel
Moment-Frame Buildings, June, 2000」 |
| |
(*1)tribで裏当て金を用いる場合は、フランジ下面と梁端水平リブの下面を同一に揃える。
(*2)ジョイントは、f の終了位置またはこれより内端側に設ける。
(*3)H法の内端リブの先端部回し溶接は省略してもよい。
|
|
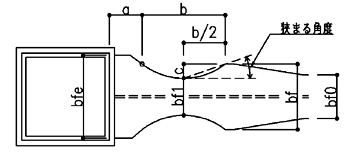
| 用語の定義 |
| 切欠き断面:梁フランジ幅がbf1となる切欠き底の断面 |
| db:梁成 |
bf 0:中央フランジ幅 |
bf:内端フランジ幅 |
| c:切欠き深さ |
bf1:切欠きフランジ幅 |
bfe:梁端フランジ幅 |
| α:梁端の幅がbf となる点 |
a:柱フェースと点αの距離 |
b:切欠き長さ |
| f :内端リブ長さ |
f1:内端リブの平行部分長さ |
r :切欠き半径 |
| t f :フランジ厚 |
Zp:切欠き断面の塑性断面係数(ウェブを考慮して算定) |
| Mf :梁端モーメント |
Zb :梁端部の塑性断面係数,Zb = t f ・bfe・(db-t f ) |
| Af1:切欠き部のフランジ断面,Af1 = bf1 ・t f |
| e:梁フランジサイドのあき寸法 |
|
| |
表2 制限範囲 |
項目 |
内容 |
梁の対称性 |
リブと切り欠き形状は対称とする。 |
梁の幅厚比 |
FAランクとする。切欠き断面においても中央フランジ幅 bf 0を用いて評価する。 |
梁の横補剛 |
保有耐力横補剛。切欠部の区間は、切欠き断面のA f 1と i yを用いて評価。梁端からの距離がa+bの範囲には、横補剛材のガセットを溶接しない。 |
[スパン/梁成]の最小値 |
[スパン/梁成] ≥ 5 |
梁中央部の幅 |
中央フランジ幅:bf 0 ≤ 300 |
フランジ厚t f |
40mm以内 |
柱との偏心 |
梁端フランジ幅 bf e 部分が柱の幅内に収まる。
偏心のない場合も同様。 |
床剛性 |
>コンクリート、デッキプレート・コンクリート、ブレースにより剛床とする。ただし、ブレースによる場合ブレース取付部のディテール等については、現状の梁端の形状や力学的挙動に影響を及ぼすことが無いものとする。 |
床スラブのスタッドコネクタ |
スタッドコネクタは、柱面と切欠部の終端から15cm内端側の間(a+b+15cm)のエリアには設置しない。 |
形状の補足 |
・点αはaとbの長さを定める点とする。
・梁端フランジ幅を、bf より拡幅する場合は、点αより円弧の概ね接線方向に延長する。梁端フランジ幅 bf e は、bf 以上とする。
・超音波探傷検査と溶接施工に関わる梁端寸法は、図3による。 |
|
| |
|
図1 ERBS-Hの形状・寸法 |
| |
|
図2 ERBS-BHの形状・寸法 |
| |
|
図3 各形式に対する梁端寸法 |
| |
| H法とBHに対する梁形状の設定フローを図4に示す。 |
|
図4 梁形状の設定フロー |
| |
(注1) ヒンジ位置の初期値は、実験値を参考に、以下の値を目安とする。

(注2) フランジの狭まる角度を、解析と実験値を参考に調整。
b/2c ≒ 2.9 |
 |
|
② 応力計算
|
| |
応力計算は、梁の切欠き形状の特性を適切にモデル化して実施する。
前記以外による場合は、以下による剛域付のフレーム解析手法によることができる。
・フレーム解析プログラムにより、切欠き断面と剛域をモデル化する。
・剛域の長さを、柱面から、a+b/2に設定。切欠き断面の長さを、b/2に設定。
・ジョイント位置を柱面からa+bに設定して、切底き断面と中央断面を区別する。
・梁の剛性には、コンクリートスラブとの合成効果は考慮しない。
|
|
|
図5 剛域付のフレーム解析 |
| |
③ 応力度の確認
|
| |
・梁端の許容曲げ応力度は、切欠き断面の bf 1 と t f を用いて算定する。
切欠き断面を有する区間の横座屈長さ lb は、柱フェース(または柱芯)と、梁端から第1番目の横補剛までの距離とする。
・断面算定位置を剛域端に設定する。
・梁に軸力が存在する場合は、切欠き断面を有する座屈区間の許容圧縮応力度を、切欠き断面における断面2次半径を用いて算定する。
|
|
④ 床版の応力集中等の確認
|
| |
梁フランジ上のスタッドコネクタは、柱面と切欠部の終端から15cm内端側の間(a+b+15cm)のエリアには設置しない。この分を勘案して床のせん断力伝達に関する安全性を確認する。検討は、当該階のブレースのせん断力を、下階で異なる通のブレース構面にスラブの面内せん断力を介して伝える必要がある部位等に対して行う。
スタッドコネクタの耐力は、「日本建築学会:各種合成構造設計指針・同解説,1985」等による。
|
|
⑤ RBS断面の検定
|
| |
梁端接合部の曲げ耐力とせん断耐力が、RBS工法の検定式を満足していることを確認する。梁端接合部は、フランジで曲げモーメントを、ウェブでせん断力を負担するものとする。
ウェブで曲げとせん断を負担する場合は、日本建築学会「鋼構造接合部設計指針」(2002年)等により評価する。
|
|
ⅰ)梁端部のモーメントに対する設計 |
| ・接合部の曲げ耐力の評価 |
| |
梁端接合部に作用する曲げモーメントを下記のよう評価する。
ここでは、梁端モーメント M f は図6~7の荷重条件とメカニズム状態に対してして定める。長期荷重の条件が異なる場合は、それに応じたせん断力 Vpを評価する。
|
|
| |
M f = Mpr+Vpx = Cpr Ry Zp Fy+Vpx (1)
Mpr = Cpr Ry Zp Fy (2)
M f :梁端(柱フェース)での必要モーメント
Mpr :予想ピーク塑性ヒンジモーメント
Cpr:歪硬化・局部拘束・付加的な補強・接合状態等によるピーク強度係数、
RBS工法に対してCpr = 1.15
Ry:梁の材料に関する(材料の基準強度の割増)係数、Ry = 1.1
Zp:切欠き断面(塑性ヒンジ位置)の塑性断面係数(ウェブを考慮して算定)
Fy:鋼材の基準強度
Vp:塑性ヒンジ位置でのせん断力
Vp = |
Mpr+Mpr+PL’/2+wL’2/2 |
|
| |
L’ |
x :塑性ヒンジと柱フェース間の距離,x = a+b/2
p:梁中央部の集中荷重
w:梁上の分布荷重
|
|
|
図6 荷重条件とヒンジ位置でのせん断力の算定
|
|
図7 柱フェースでのモーメント
|
| ・接合部曲げ耐力の検定 |
| |
下記の要件を満たせば、設計は許容可能となる。
M f < Ry Zb Fy (4)
Zb:梁端部の塑性断面係数, Zb = tf ・bfe ・(db-t f )
|
|
| ⅱ) 接合部のせん断力に対する設計 |
| |
次の式により、柱面でのせん断力 Vf を計算する。
τ = Vf /tw(db-2t f-2Sr )
τ/fs ≦ 1.0
ここに、
QⅬ: 長期荷重によるせん断力
fs : 許容せん断応力度
Sr: スカラップの寸法
その他、パネルゾーンおよびダイアフラムについては、「鋼構造設計規準」,「鋼構造接合部設計指針」等により評価する。
|
|
⑥ 層間変形角の確認
|
| |
応力計算で用いた“剛域付のフレーム解析”により層間変形角を評価した場合、梁の可撓長さが小さくなり実際より変位が小さめに算定される。このため、安全側の評価となる以下の略算により別途確認する。(変位を精算する場合は、別途変断面梁モデル等により評価する。参考資料Aに、変断面のビーム要素を用いたフレーム変位の検討結果を示す。)
・梁部材を一様鉄骨梁断面の要素でモデル化する。この断面は、中央部の鉄骨断面とする。梁の剛性には応力計算と同様に、コンクリートスラブとの合成効果は考慮しない。
・算出した変位から、層間変形角が許容値以内であることを確認する。
この一様鉄骨梁のフレーム変位は、RBS断面を考慮した実際の精密解析より、大きめの水平変位を与えるため安全側の評価となる。
梁のたわみも同様に、一様鉄骨梁のフレームのたわみが実際より大きめとなるため、安全側となる。
|
|
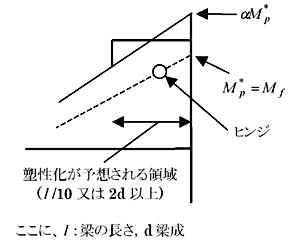
⑦ 接合部の破断防止
|
梁端の保有耐力接合の確認を、以下のように行う。
・仕口部設計用曲げモーメント
| |
保有水平耐力時に梁部材に作用する応力は、梁端での必要モーメントM f となる。
この応力に安全率αを乗じて仕口部が破断しないことを確認する。M fには、安全側に長期応力と Cprを考慮している。
仕口部設計用曲げモーメントαM*pは、
αM*p = αMf = (Cpr Ry Zp Fy+Vpx)
|
 |
|
・仕口部最大曲げ強度の検定
| |
仕口部設計用曲げモーメントを αM*p として、梁端仕口部が破断しないことを確認する。ただし、RBS断面の検定を材料の降伏強さで行っているため、下記の検討により満足される。
RBS断面の検定式の両辺に安全率αを乗じて、
α(Ry Zb Fy) > αM f = αM*p
(400N級炭素鋼:α = 1.3)
ZbσU = 400 Zb > α(Ry Zb Fy)=1.3×1.1 Zb×235=336 Zb > αM*p OK
(490N級炭素鋼:α = 1.2)
ZbσU = 490 Zb > α(Ry Zb Fy) =1.2×1.1 Zb×345=455 Zb > αM*p OK
|
|
⑧ 局部座屈等の防止
|
梁の保有耐力横補剛の確認を、以下のように行う。
・“はり全長にわたって均等間隔で横補剛を設ける方法” を準用する場合
| |
端部の横補剛間隔は l/ne 以内とする。 ne は、切欠き断面の梁の弱軸まわりの細長比 λye が、次式を満足する横補剛数とする。
λye ≦ 170+20 ne (400N級炭素鋼梁の場合)
λye ≦ 130+20 ne (490N級炭素鋼梁の場合)
中央の横補剛間隔は l/nc 以内とする。 nc は、中央断面の梁の弱軸まわりの細長比 λyc が、次式を満足する横補剛数とする。
λyc ≦ 170+20 nc (400N級炭素鋼梁の場合)
λyc ≦ 130+20 nc(490N級炭素鋼梁の場合)
ここに、l :梁の長さ
λye:切欠き断面の梁の弱軸まわりの細長比( = l/iye)
λyc:中央断面の梁の弱軸まわりの細長比( = l/iyc)
iye:切欠き断面に関する梁の弱軸まわりの断面2次半径,√(I y1/A1 )
iyc:中央断面に関する梁の弱軸まわりの断面2次半径,√(I y/A)
I y1,I y:梁の切欠き断面と中央断面に関する弱軸まわりの断面2次モーメント
A1,A:梁の切欠き断面と中央断面の面積
|
|
・“主として梁端部に近い部分に横補剛を設ける方法” を準用する場合 |
| |
降伏曲げモーメントを超える曲げモーメントが作用する領域においては、次式で示す間隔で横補剛を配置する。ただし、梁の横補剛を検討するためのモーメント分布は、柱フェースでのモーメントが Mf であるとして評価する。また、降伏曲げモーメントは、端部では切欠き断面のものを、中央では中央断面のものを用いる。
梁の横補剛を検討するための曲げモーメント分布には、安全率αを乗じたものを用いる。安全率αは、400N級炭素鋼梁でα = 1.2とし、490N級炭素鋼梁でα = 1.1とする。
400N級炭素鋼の梁の場合
| 端部の横補剛間隔: |
|
≦ 250 かつ |
|
|
|
|
Af1 |
iye |
| 中央の横補剛間隔: |
|
≦ 250 かつ |
|
|
|
|
Af 0 |
iyc |
490N級炭素鋼の梁の場合
| 端部の横補剛間隔: |
|
≦ 200 かつ |
|
|
|
|
Af1 |
iye |
| 中央の横補剛間隔: |
|
≦ 200 かつ |
|
≦ 50 |
|
|
Af 0 |
iyc |
Af1:切欠部のフランジ断面, Af1 = bf1・t f
Af 0:中央のフランジ断面, Af0 = bf 0・t f
lbe:切欠部を有する梁端部の横補剛間隔
lbc:中央断面の梁の横補剛間隔
|
|
⑨ 保有水平耐力の確認
|
| |
保有耐力算定時の梁の塑性ヒンジは、切欠き断面位置に生じるものとする。保有耐力の算定時は、梁の耐力にCprの割増しは行わない。
フレーム解析プログラムにより計算する場合は、1次設計の応力算定と同じ剛域モデルにより算定してもよい。
|
|